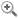Graver des figures de géométrie au XIXe
siècle : pratiques, enjeux et acteurs éditoriaux
- Norbert Verdier
_______________________________
Dulos ne se contente pas de faire de la gravure sur cuivre ; il améliore les procédés. Avant lui, les gravures en creux provoquaient, après encrage et transfert sur la page, des tracés qui n’étaient pas toujours nets. Il améliore chimiquement le procédé au début des années soixante en tentant d’avoir un aval académique. En 1863, par l’intermédiaire de Claude-Servais-Mathias-Marie-Roland Pouillet (1790-1868), il soumet une « Note sur de nouveaux procédés de gravure en creux et en relief » et « met sous les yeux de l’Académie divers spécimens des planches obtenues par ces procédés, et des épreuves qu’on en a tirées » [102]. Il est statué : « Cette Note, trop étendue pour pouvoir être reproduite intégralement au Compte rendu, et qui doit être l’objet d’un prochain Rapport, est renvoyée à l’examen d’une Commission composée de MM. Pouillet, Fremy et Fizeau » [103]. Les Comptes rendus ne mentionnent pas l’existence d’un tel rapport. Dulos n’a pas la certification académique recherchée. Plus tard, dans le dernier tiers du XIXe siècle, certains travaux améliorant l’art de la photographie – comme ceux Niepce – s’inspirent des travaux initiaux de gravure de Dulos. Avec Dulos, la gravure atteint sa maturité et entre dans une autre histoire, celle de sa pré-industrialisation : les burins des graveurs sont définitivement remplacés par des procédés chimiques qui rendent possible l’insertion des figures à des coûts accessibles et avec une netteté graphique irréprochable. A l’exposition universelle de 1855, Dulos présenté comme « dessinateur et graveur en titre de l’Ecole polytechnique », est récompensé d’une « médaille de 2e classe ». « Pour les gravures à l’usage des démonstrations scientifiques, l’effet artistique est moins ce que les professeurs et les élèves doivent trouver dans une gravure que l’exactitude des projections, la précision du trait, ainsi que la justesse de la perspective et des ombres » [104], souligne le jury. Dulos fait partie des graveurs qui ont éliminé l’effet artistique pour se consacrer à l’efficience du trait.
Et les autres
En étudiant les productions des graveurs dont le nom figure dans la presse mathématique, nous n’avions pas la prétention de rendre compte exhaustivement de tout ce qui se passe en matière de lithographie mathématique. D’autres graveurs produisent des figures mathématiques sans intervenir forcément dans la presse mathématique. Pour les identifier, nous avons systématiquement consulté la production mathématique en France en désignant par mathématique tout ce que les libraires qualifiaient de mathématiques dans leurs différents journaux bibliographiques [105]. Par ce choix d’acteurs (les libraires), les livres de mathématiques offrent une grande diversité allant du livre de calcul élémentaire destiné aux élèves aux traités les plus techniques produits par de grands savants sans omettre de nombreux ouvrages – comme les tables numériques ou géométriques – à destination de multiples professions (des métiers du bois, de l’artillerie ou des multiples champs de l’ingénierie dévéloppés au cours de la Révolution industrielle). La table ci-dessous présente les principaux graveurs pour les mathématiques que nous avons repérés par notre méthodologie (fig. 15).
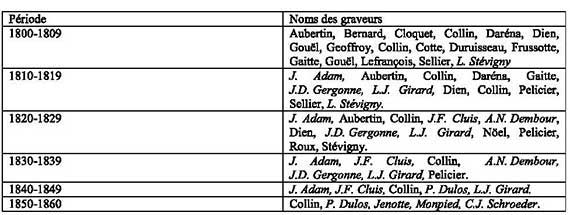
Fig. 15. Les principaux graveurs intervenant dans les livres de mathématiques (1800-1860).
Parmi ces graveurs, plusieurs interviennent peu, seulement durant quelques années ou bien pour quelques ouvrages ; d’autres sont plutôt spécialisés dans la représentation des cartes géographiques et, à ce titre, leur intervention dans le domaine des mathématiques reste marginale. C’est le cas d’Alphonse Pelicier et surtout de la dynastie Collin [106]. Les autres, ceux dont le nom est indiqué en italiques, sont au cœur de cet article et de nos préoccupations.
Les graveurs de la presse de vulgarisation
Focalisons-nous sur un type de presse très avide d’illustrations : la presse de vulgarisation qui se développe à tout va au cours du XIXe siècle. Nous allons ici nous intéresser aux figures de géométrie insérées dans deux journaux de vulgarisation différents l’un de l’autre ; ils montrent l’extrême diversité de cette « presse de vulgarisation » à propos de laquelle Marie-Laure Aurenche précise :
Dans un siècle marqué par les bouleversements politiques, les progrès techniques et la généralisation de l’instruction, l’expression moderne de « presse de vulgarisation » est impropre pour désigner toutes les publications qui ont diffusé les connaissances au XIXe siècle. Si les recueils hebdomadaires, mensuels ou annuels appartiennent effectivement à la presse, les encyclopédies, collections et dictionnaires qui paraissent par livraisons, volumes ou tomes successifs, ne peuvent figurer sous l’étiquette de « presse », même périodique [107].
Le premier journal choisi est le Journal des connaissances usuelles et pratiques ou le Recueil des notions immédiatement utiles aux besoins de la société et mises à la portée de toutes les intelligences. Il a été fondé par le philanthrope Charles-Philibert de Lasteyrie (1759-1849) et appartient à la première composante de la presse de vulgarisation « classique » mise en avant par Marie-Laure Aurenche. Les articles de géométrie sont essentiellement dus à Didiez, successeur, nous l’avons précisé, du baron Pierre-Charles-François Dupin (1784-1873) au Conservatoire national des arts et métiers. La deuxième publication périodique est l’Encyclopédie moderne, dictionnaire abrégé des sciences, des lettres, des arts, de l’industrie, de l’agriculture et du commerce. Lancée à la fin des années quarante, elle est constitutive de la deuxième composante de la presse de vulgarisation pointée par Marie-Laure Aurenche. Les mathématiques de l’Encyclopédie sont écrites par Francœur, qui a aussi écrit pour le Journal des connaissances usuelles et pratiques. Parmi les signataires de l’Encyclopédie, figure un des auteurs importants de la presse scientifique : Jacques-Frédéric Saigey (1797-1871) [108]. Il est présenté sous le titre « Saigey, professeur de mathématiques » mais il écrit, pour l’Encyclopédie, non des articles de mathématiques – quasiment exclusivement confiés à Louis-Benjamin Francœur (1773-1849) – mais plutôt des articles de chimie ou de physique comme lorsqu’il écrivait, à ses débuts, pour le Bulletin de Férussac des comptes-rendus des Annales de physique et chimie.
Le Journal des connaissances usuelles et pratiques insère, dans le corps du volume parfois mais beaucoup plus généralement en fin de volume, quelques planches explicatives, exécutées par le lithographe Jacques François Cluis [109]. Les planches relatives à un texte non mathématique sont presque toujours constituées de très peu de figures, souvent une seule, porteuse d’assez peu d’informations. Elle est là à titre d’illustration. Ainsi la planche intitulée « Nouvelle presse typographique à toucheur mécanique de Mr Selligue » [110] montre deux ouvriers actionnant la presse en question. Les planches de géométrie (non signées) sont composées de multiples figures, à vertu explicative. Par exemple, la planche insérée dans le tome 5, n°26 de mai 1827 est composée de vingt-deux figures numérotées. Elle accompagne un article de Didiez intitulé « Principes de géométrie » qui se poursuit dans les fascicules de juin 1827 et juillet 1827 [111]. L’article de juin est également accompagné d’une planche de figures qui sont numérotées de 23 à 43 ce qui signifie qu’au total ce mémoire de trente et une pages est accompagné de quarante-trois figures (souvent très élémentaires) (fig. 16).
Dans le cahier mensuel, les figures étaient disposées sur une feuille volante, qui, comme pour Le Géomètre, était insérée à l’intérieur du fascicule. Dans le dernier article, en dernière page, une note mentionne : « L’auteur de cet article, M. N. J. Didiez, professeur de mathématiques pures et appliquées, fera paraître sous peu un Cours complet de Géométrie, divisé en quatre parties, formant 4 vol. in-° qui seront publiés séparément et successivement » [112]. Dans le cahier d’août 1827 et de septembre 1827, Didiez poursuit ses « principes de géométrie ». Ses articles sont accompagnés de planches. Il annonce que la suite est à venir. Au total, la participation de Didiez – qui vient de publier Résumé d’un cours de mathématiques pures, ouvert le 24 novembre 1825 [113] – dans le tome 5 du Journal des connaissances usuelles et pratiques, entre mai et septembre 1827, occupe quarante-quatre pages et fait appel à soixante-huit figures. L’étude des figures du Journal des connaissances usuelles et pratiques fait ressortir une fonction différente des planches suivant qu’elles traitent ou non de mathématiques. Les (nombreuses) planches de mathématiques ont une fonction explicative alors que les autres planches ont une fonction qui relève quasi exclusivement de l’illustration. L’éditeur s’adresse à des lecteurs qui ne sont pas « versés dans l’étude des mathématiques ».
[102] P. Dulos, « Note sur de nouveaux procédés de gravure en creux et en relief », Comptes rendus hebdomadaires des séances de l’Académie des sciences, 56 (1863), p. 127.
[103] Ibid.
[104] Rapports du jury mixte international publiés sous la direction de S.A.I. le prince Napoléon, Paris, imprimerie impériale, 1856, p. 1273.
[105] Pour plus d’informations sur le qualificatif de « livre mathématique », voir N. Verdier, « Editer des mathématiques avec des libraires : imbrications, enchaînements et innovations », dans Sciences mathématiques 1750-1850 : continuités et ruptures, sous la direction de C. Gilain et d’A. Guilbaud, Paris, Ed. du CNRS, à paraître. Ce texte présente aussi la méthodologie pour identifier les libraires produisant des mathématiques. Ici, nous l’adaptons pour identifier les graveurs de mathématiques.
[106] O. Chapuis, A la mer comme au ciel. Beautemps-Dupré & la naissance de l’hydrographie moderne (1700-1850), « Histoire maritime », Paris, Presses de l’université Paris-Sorbonne, 1999.
[107] M. L. Aurenche, « La presse de vulgarisation ou la médiation des savoirs » dans La Civilisation du journal. Histoire culturelle et littéraire de la presse française au XIXe siècle, dirigé par D. Kalifa, P. Régnier, M-E. Thérenty et A.Vaillant, Paris, Nouveau monde éditions, 2011, pp. 383-415.
[108] Pour une courte biographie de Saigey et une étude de son rôle dans le Bulletin des sciences de Férussac, voir A. A. Cournot. Œuvres complètes, dirigé par B. Bru et T. Martin, tome XI, vol.1 & 2, Ecrits de jeunesse et pièces diverses, Librairie Vrin & Presses universitaires de Franche-Comté, 2010, pp. 579-590. Pour son rôle par contre-réaction dans la création des Comptes rendus hebdomadaires de l’Académie des sciences, voir B. Belhoste, « Arago, les journalistes et l’Académie des sciences dans les années 1830 », dans La France des années 1830 et l’esprit de réforme, dirigé par P. Harismendy, Rennes, PUR, 2006, pp. 253-266.
[109] Jacques François Cluis a obtenu son brevet de lithographe en 1826 ; il a succédé à Auguste, Léon Macaire célèbre pour ses opinions libérales et « son mauvais esprit anti-royaliste » (Archives nationales, F/18/1797). Le Journal des connaissances usuelles et pratiques consacre un article intitulé « Autographie » dans lequel sont détaillés les apports de l’imprimeur-lithographe Cluis (Journal des connaissances usuelles et pratiques, 61 (Avril 1830), pp. 164-167).
[110] Journal des connaissances usuelles et pratiques, 81 (décembre 1830).
[111] N. J. Didiez, « Principes de géométrie », Journal des connaissances usuelles et pratiques, 26 (Mai 1827), pp. 49-62; 27 (Juin 1827), pp. 97-104 ; 28 (Juillet 1827), pp. 145-153, 29 (Août 1827), pp. 193-199 et 30 (Septembre 1827), pp. 241-246.
[112] Ibid., p. 153.
[113] N. J. Didiez, Résumé d’un cours de mathématiques pures, ouvert le 24 novembre 1825, Paris, chez l’auteur et chez Bachelier, 1826.