
Graver des figures de géométrie au XIXe
siècle : pratiques, enjeux et acteurs éditoriaux
- Norbert Verdier
_______________________________
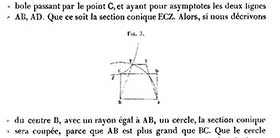
Fig. 6. Fr. Woepcke, « Sur la construction des équations
du quatrième degré… »,
Journal de mathématiques
pures et appliquées, 1863 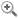
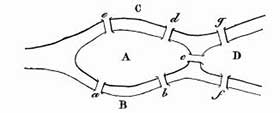
Fig. 8. Le problème des ponts de Koenigsberg,
Nouvelles annales de mathématiques, 1851 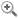
De plus, l’éditeur a le souci constant d’éviter autant que faire se peut la réalisation de planches. Cela semble être une préoccupation omniprésente chez Bachelier. Souvent, dans les articles, la volonté explicite d’économiser des illustrations « in texte » et de se limiter à quelques planches reliées en fin de volume est sous-jacente. Nous allons examiner deux exemples montrant explicitement cette volonté d’éviter les figures. Le premier exemple concerne un échange épistolaire entre Théodore Bailleul (1797-1875), le directeur de l’imprimerie mathématique de Bachelier [45], et Franz Woepcke (ou Wöpcke sous sa forme allemande) (1826-1864), un auteur important du Journal de Liouville [46]. Cet échange montre que c’est Bailleul en personne qui insiste auprès de l’auteur pour éviter les figures. Bailleul écrit en 1862 à Woepcke : « Monsieur, je vous prie de me dire s’il est indispensable de faire graver les 3 figures. J’ai l’honneur de vous saluer avec respect, Bailleul » [47]. Woepcke insiste pour le maintien des figures dans son texte : « Les figures sont indispensables à l’intelligence du texte. Si vous pouvez les reproduire autrement que par la gravure cela m’est indifférent. Je pourrais, si cela était très nécessaire, remplacer les trois figures par une seule » [48]. Cet échange concerne un article pour le Journal de Liouville : « Sur la construction des équations du quatrième degré par les géomètres arabes » [49]. Le manuscrit original – annoté par Liouville – se trouve dans le fonds Woepcke [50]. En dessous du titre, Liouville a rajouté le nom de l’auteur ainsi que : « Une épreuve pour Mr Woepcke, rue Bréa, N° 20, et une pour moi. JL ». Il a également porté l’indication faisant office de bon à tirer : « Pour le journal de mathématiques – à imprimer tout de suite. JL ». Le manuscrit comporte plusieurs annotations : « 3 figures à graver (Mr Claudel) » [51]. Au final, les trois figures sont effectivement éditées dans le corps du texte (fig. 6).
Cet exemple n’est pas uniquement intéressant par la (vaine) tentative d’évitement des figures, il l’est aussi parce qu’il fait entrer un nouvel acteur dans la réalisation des figures géométriques. Les figures de l'article de Woepcke ont été gravées par Joseph Claudel (1815-1880). Ingénieur de l’Ecole centrale des manufactures, il est l’auteur de plusieurs ouvrages techniques et est l’inventeur d’un nouveau procédé simple de gravure [52] qui s’est répandu dans le milieu de l’édition au cours des années 1860. Les figures réalisées par Claudel ne sont pas signées mais sa présence est attestée dans divers avertissement. Par exemple, Poncelet ouvre ses Applications d’analyse et de géométrie qui ont servi de principal fondement au Traité des propriétés projectives des figures (avec additions de Victor-Mayer-Amédée Mannheim (1831-1906) & Théodore-Florentin Moutard (1827-1901)) en soulignant le rôle joué par l’imprimerie mathématique de Mallet-Bachelier « si bien dirigée par notre célèbre prote » (Bailleul) [53] et insiste sur « l’aide de M. Claudel, artiste aussi ingénieux qu’instruit, inventeur d’un nouveau système de gravure, et auteur d’ouvrages fort appréciés sur l’art de l’ingénieur » [54].
Le deuxième exemple concerne des articles d’Adémar-Jean-Claude Barré de Saint-Venant (1797-1886), un autre auteur important du Journal. C’est cette fois Liouville qui exige de l’auteur le moins de figures possible à propos d’un article de Saint-Venant de 1863. Le 15 mars 1863, Liouville écrit : « Le moins de figures que vous pourrez, bien entendu, en restant clair » [55]. Saint-Venant a respecté les volontés de Liouville à propos des figures géométriques. Son texte ne comporte que deux figures « in texte » [56]. Ont-elles été exécutées par Claudel ?
A côté de ces deux exemples pour lesquels nous avons des archives montrant les pressions de Bailleul et de Liouville pour éviter les figures, il est possible de voir dans le corps du texte cette stratégie d’évitement. Nombreux sont les textes pour lesquels une figure est utilisée à plusieurs reprises sans être reproduite. Voici un exemple parmi tant d’autres possibles. En 1849, Wantzel [57] fait paraître à titre posthume un article de géométrie que nous avons par ailleurs étudié [58]. L’article comprend douze pages et une seule figure « in texte », en deuxième page. Cette illustration sert de référence dans le reste du texte à deux reprises. En page 114, une note de bas de page précise « On peut suivre sur la même figure » ; en page 116, une autre note de bas de page insiste « Même figure ». Cette façon de faire n’est pas une particularité de cet article (composé très rapidement pour rendre hommage à un géomètre disparu quelques mois plus tôt) mais est assez courante dans le Journal où tout est fait pour éviter, dans la mesure du possible, les figures géométriques.
Changement d’éditeur aux Nouvelles annales de mathématiques ou vers moins de planches
La stratégie d’évitement est particulièrement mise en uvre quand Bachelier reprend la gestion des Nouvelles annales en 1849. De 1842 à 1848, les Nouvelles annales sont publiées par Carilian- Gœry (ou Gœury) et Victor Dalmont ; dans le septième tome (1848), un changement d’éditeur est annoncé :
A partir de janvier 1849, on devra adresser les demandes d’abonnement à M.Bachelier, libraire, quai des Augustins. Il n’est rien changé aux conditions. MM. Carilian- Gry et Dalmont (Victor), anciens éditeurs, serviront les abonnés qui ont déjà souscrit chez eux pour 1849 [59].
Le nouvel éditeur, Bachelier, revendique un esprit de continuation :
Nous ne négligerons rien pour que les Nouvelles annales, remplissant le but de leur fondation, paraissent mensuellement avec exactitude, et que l’exécution typographique, ainsi que celle des planches, répondent de plus en plus aux vux des abonnés [60].
Au niveau de la typographie, il y a une continuité éditoriale malgré le changement d’éditeur ; en revanche, au niveau des planches, il y a une rupture comme l’atteste le tableau suivant (fig. 7).
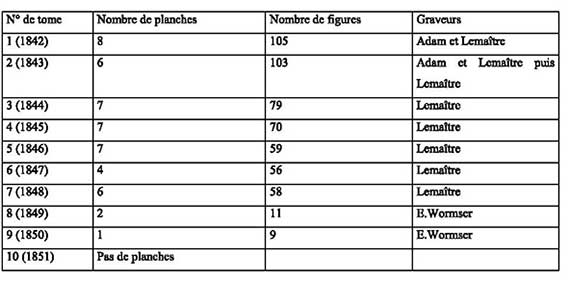
Fig. 7. Nombre de planches et de figures dans les Nouvelles annales de mathématiques (entre 1842 et 1851) & noms des graveurs.
A partir de 1849, le nombre de planches et de figures chute de manière vertigineuse. Elles disparaissent quasiment du journal à partir des années cinquante. Il convient toutefois d’indiquer que la disparition ou du moins la restriction du nombre de figures dans les planches en fin de volume ne signifie pas qu’il n’y a pas d’illustrations « in texte », mais pas depuis le début de la publication. Dans le premier tome, en 1842, il n’y a pas de figures « in texte ». C’est la même chose dans le cinquième tome en 1846. Il semble que sur la période 1842-1848, toutes les figures sont insérées dans les planches en fin de volume. En revanche, dès que Bachelier prend la responsabilité éditoriale, le nombre de planches diminue mais il peut y avoir des planches « in texte ». Par exemple, dans le dixième tome, en 1851, il n’y a pas de planche mais il y a douze figures « in texte » dont trois illustrent un texte d’Emile Coupy premier traducteur en français du célèbre problème de Leonhard Euler (1707-1783) à propos des ponts de Koenigsberg [61] (fig. 8).
Même s’il y a quelques figures « in texte », il y en a incontestablement moins. Sur la période 1842-1848, nous dénombrons une moyenne d’environ soixante-seize figures par volume. Qu’en est-il ensuite ? Nous nous contentons d’un pointage statistique en étudiant le tome X (1851), le tome XV (1856) et le tome XX (1860). En 1851, nous en comptons douze. Cette volonté d’éliminer les figures transparaît dans le corps du texte. A titre d’exemple, un article d’Edouard Terré (1832-1913) est consacré à une étude de positionnement de cercles. Dès le début du texte, il est précisé « On est prié de faire la figure » [62]. Dans le quinzième tome, en 1856, nous comptons treize figures « in texte ». Aucune figure n’est insérée dans le Bulletin de bibliographie, d’histoire et de biographie mathématiques [63]. Dans le vingtième tome, en 1861, il y a un peu plus de figures « in texte », vingt-et-une figures, certes, plus que dans les autres tomes étudiés mais beaucoup moins que dans la période 1842-1848. Il n’y en a aucune dans le Bulletin. Cette chute du nombre de figures (après 1848) n’est pas liée à un changement de nature du journal qui reste un journal de préparation à l’Ecole polytechnique et par là même un journal dans lequel la géométrie joue un rôle prépondérant [64]. Le lecteur des Nouvelles annales devait incontestablement lire, « un crayon à la main », pour compléter par des figures les démonstrations imprimées. Une note du rédacteur termine ainsi un article de Guillaume-Jules Hoüel (1823-1886) sur le polygone régulier à dix-sept côtés : « La très-bonne [sic] figure jointe à cet écrit ayant besoin d’être réduite, nous la supprimons. La description est si claire, que chaque géomètre peut tracer ou faire tracer la figure. Toutefois, si l’on réclame, nous la donnerons plus tard » [65]. S’ouvre alors tout un questionnement sur les pratiques de lectures de la presse mathématique.
[45] N. Verdier, « Théodore Bailleul (1797-1875) ou le prote devenu directeur de l’Imprimerie Mathématique de (Mallet)-Bachelier (1812-1864) », Histoire et civilisation du livre, IX (2013), pp. 251-269.
[46] N. Verdier, « Qui est le mathématicien et historien des mathématiques Franz Wöpcke (1826-1864) ? Qu’écrit-il ? Etoù ? », 18th Novembertagung on the History, Philosophy & Didactics of Mathematics, Mathematical Practice & Development throughout History, édité par Ingo Witzke, Logos Verlag, Berlin, λογος, pp. 257-269.
[47] Fonds F. Woepcke, Bibliothèque de l’Institut de France, MS 22 36, lettre 138.
[48] Ibid.
[49] F.Woepcke, « Sur la construction des équations du quatrième degré par les géomètres arabes », Journal de mathématiques pures et appliquées, II, 8 (1863), pp. 57-70.
[50] Fonds F. Woepcke, Bibliothèque de l’Institut de France, MS 22 39.
[51] Le manuscrit comporte d’autres annotations nominatives. Les noms de Jacques-Philippe-Marie Binet (1786-1856) et Campion reviennent à plusieurs reprises.
[52] P. Lemerre, « Claudel (Joseph) », Dictionnaire de biographie française, sous la direction de Prevost, Michel, Balteau, Jules & Barroux, Marisu, 8, col. 1384, Ed. Letouzey & Ané, 1959.
[53] J.-V. Poncelet, Applications d’analyse et de géométrie qui ont servi de principal fondement au Traité des propriétés projectives des figures (avec additions de MM. Mannheim & Moutard), tome premier, Paris, Mallet-Bachelier, 1862, p.xiii.
[54] Ibid.
[55] Fonds J. Liouville, Bibliothèque de l’Institut de France, MS 36 29/12.
[56] A.-J.-C. Barré de Saint-Venant, « Mémoire sur la distribution des élasticités autour de chaque point d’un solide ou d’un milieu de contexture quelconque, particulièrement lorsqu’il est amorphe sans être isotrope (Premier article) », Journal de mathématiques pures et appliquées, II, 8 (1863), 257-295 & « Mémoire sur la distribution des élasticités autour de chaque point d’un solide ou d’un milieu de contexture quelconque, particulièrement lorsqu’il est amorphe sans êtreisotrope (Deuxième article) », Journal de mathématiques pures et appliquées, II, 8 (1863), pp. 353-430.
[57] P. L. Wantzel, « Mémoire sur la théorie des diamètres rectilignes des courbes quelconques », Journal de mathématiquespures et appliquées, I, 14 (1849), pp. 111-122.
[58] N. Verdier, Le Journal de Liouville …, Op. cit., pp. 241-268.
[59] Nouvelles annales de mathématiques, I, 7 (1848), pp. 450-451.
[60] Ibid., I, 8 (1849), p. 5.
[61] Notons que la traduction est complétée par une adaptation de ce problème aux ponts de Paris (sans adjonction de figure) et insistons sur le fait que ce problème de graphe est un des points fondateurs d’une notion cruciale en mathématiques, la topologie.
[62] E. Terré, « Enveloppe d’une tangente à deux cercles variables », Nouvelles annales de mathématiques, I (10), 1851, pp.340-344.
[63] En 1855, Terquem – le co-fondateur, en 1842, des Nouvelles annales de mathématiques ou Journal des candidats aux Ecoles polytechnique et normale – décide d’adjoindre un Bulletin de Bibliographie, d’Histoire et de Biographie mathématiques qui compte entre une centaine et deux cents pages. Relié annuellement à la suite des Nouvelles annales, avec une pagination séparée, il constitue, sans doute, le premier journal d’histoire des mathématiques.
[64] N. Verdier, Le Journal de Liouville et la presse de son temps …, Op. cit., partie III.
[65] J. Hoüel, « Sur le polygone régulier de dix-sept côtés », Nouvelles annales de mathématiques, I (16), 1857, pp. 310-311.


