
Graver des figures de géométrie au XIXe
siècle : pratiques, enjeux et acteurs éditoriaux
- Norbert Verdier
_______________________________
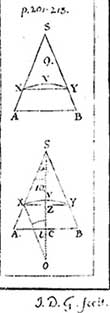
Fig. 1 a, b et c . J. D. Gergonne, Annales de
mathématiques…, 1827-1828 

Fig. 2. J. D. Gergonne, Triangle de Burg, Annales de
mathématiques, 1827-1828 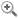
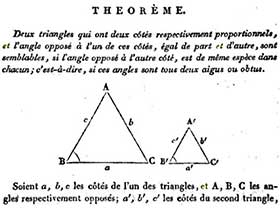
Fig. 3. J. G. Garnier, Deux triangles,
Correspondance mathématique…, 1825 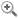
Pour graver des figures de géométrie, les graveurs utilisent essentiellement la technique dite de la « gravure en taille-douce » dont nous pouvons trouver une description détaillée dans l’article de Jean Duchesne dit Duchesne aîné (1779-1855) dans l’Encyclopédie moderne de Didot [16]. C’est une technique ancienne remontant, au moins, au XVe siècle. Elle consiste à graver le motif sur le métal, notamment du cuivre ou du zinc, avec une pointe sèche ou un burin. L’encre appliquée sur la planche de métal est retenue par les sillons, si bien que le papier pénètre dans les sillons et absorbe l’encre sous l’effet de la presse. Plus tard, au XVIe siècle, le procédé est amélioré. Au lieu de graver directement le cuivre, la plaque de cuivre est recouverte d’une couche de vernis. Ensuite, l’artiste grave cette couche sans toucher le métal. La plaque est ensuite plongée dans un bain d’acide en vue d’une « morsure sélective ». L’acide joue le rôle du burin de l’ancienne technique en attaquant les parties du métal mises à jour par la gravure sur le vernis. Le temps d’immersion détermine la profondeur des creux et l’intensité des traits lors du tirage sur papier. Il suffit ensuite de rincer la plaque et de retirer le vernis. L’encrage et l’impression sont, pour finir, effectués classiquement. Entre le XVIe et le XIXe siècles, la technique évolue peu du moins au cours des deux premiers tiers du XIXe siècle. Les graveurs de géométrie sont des héritiers assez directs d’Abraham Bosse (1602-1676) [17] et de son Traité des manières de graver en taille-douce sur l’airain par le moyen des eaux fortes et des vernis durs et mols, d’imprimer les planches et de construire la presse [18].
Publier des textes de mathématiques requiert souvent l’utilisation de figures géométriques pour la compréhension du texte. Ces figures peuvent être insérées dans le texte, mais cela est techniquement difficile. Il faut insérer dans le texte une plaque gravée à l’échelle de la figure à insérer. Tout le reste du texte doit ensuite être composé en tenant compte de cette insertion. Toute proportion gardée, c’est similaire à ce que nous faisons aujourd’hui lorsque nous insérons dans du texte une image, à une différence près qui est fondamentale, c’est que nous avons la possibilité de « zoomer » et d’adapter automatiquement la taille de la figure. Les typographes du XIXe siècle devaient préalablement organiser spatialement la page avant d’en définir les composants et d’en exécuter la réalisation. La seconde solution est de regrouper les figures dans des planches réunies en fin de volume sous forme de dépliant. Souvent, dans les versions reliées d’un journal (en bibliothèques ou dans les versions numérisées), les planches sont omises. Cela induit des recherches supplémentaires [19] pour retrouver des tomes reliés possédant les planches initiales. L’exécution graphique des planches était techniquement plus simple puisque le graveur disposait d’une plaque entière (souvent de cuivre) sur laquelle il lui suffisait de disposer ses figures. A la fin de ce paragraphe, nous donnons un exemple de figure in texte, extraite d’un texte de Gaspard-Gustave Coriolis (1792-1843) [20] ouvrant le premier tome du Journal de Liouville, en 1836.
L’insertion de planches en fin de volume, en revanche, peut rendre la lecture difficile puisque, à chaque étape du texte, il faut se référer aux planches. Un jeu de va-et-vient, entre le corps du texte et les planches, s’effectue. Pour rendre la lecture plus facile, les éditeurs commencent le dépliant des planches par une page blanche repliée en accordéon. Ainsi, en dépliant la planche, le texte et les figures sont dépliés en vis à vis. Cette façon de faire n’est pas réservée aux journaux mathématiques. Les manuels utilisent également assez systématiquement ce procédé. Ce procédé est finalement une façon astucieuse de contourner le problème. Les figures « hors texte » deviennent « in texte ».
Nous allons passer en revue les différents journaux mathématiques de la première moitié du XIXe siècle pour étudier les diverses pratiques utilisées en ce qui concerne l’insertion des figures.
Gergonne : fondateur, rédacteur et graveur des Annales de mathématiques
pures et appliquées
Les Annales de Gergonne utilisent deux types d’insertion. Le premier type, le plus courant, est l’insertion sous forme de planches en fin de volume (fig. 1 a, b et c). La figure porte la mention « J.D.G. fecit » car elle a été réalisée par Gergonne lui-même, comme toutes les figures des Annales [21]. Comme le montre notre illustration, en dépliant la planche, grâce au décalage par rapport à la tranche du livre, le lecteur peut, sans gêne, lire l’article en question auquel est associée la figure.
Le deuxième type d’insertion, qui est beaucoup plus rare consiste à insérer des figures élémentaires (triangles, carrés, etc.) dans le corps du texte. Nous avons joint un exemple (fig. 2). Elle accompagne un commentaire (critique) de Gergonne sur une démonstration d’un professeur de Vienne, le professeur Adam Freiherr von Burg (1797-1882) [22]. Le texte initial a été publié (sans figure associée) dans le Journal de Crelle [23]. Nous pouvons remarquer le manque de finition de la figure insérée dans les Annales : les sommets ne coïncident pas exactement et cela n’est pas dû au mauvais encrage mais à la mauvaise réalisation dans la gravure initiale. Les segments des triangles sont mal accolés. Nous ignorons si ces figures élémentaires sont réalisées par Gergonne. Elles ne sont pas signées mais de fortes présomptions inclinent à faire penser qu’il en est l’auteur. Il est également important de remarquer une insertion totale au sens suivant : le typographe a seulement laissé de la place (en procédant à un décalage vertical). Il n’a pas composé son texte autour de la figure mais seulement avant et après.
Une économie de figures dans la presse d’Outre-Rhin
L’exemple précédent, faisant référence au Journal de Crelle, semblait montrer que l’éditeur allemand cherchait à éviter l’insertion des figures : le texte de Burg, appuyé sur un raisonnement géométrique, nécessitait une figure, ce que Gergonne a fait dans ses Annales. Le premier tome du Journal de Crelle est composé par Carl-Friedrich-Wilhelm Duncker (1781-1869) & Peter Humblot (1779-1828) ; les suivants le sont par Georg-Andreas-Reimer (1776-1842). Ils suivent la même politique éditoriale en matière de planches en insérant une table de quelques figures (non signées) pour chaque cahier. Si nous examinons rapidement la production allemande (en incluant le journal de Vienne, Zeitschrit für Physik und Mathematik), nous constatons qu’il y a très peu de figures et que rien n’est fait pour faciliter la lecture. Les éditeurs viennois du Zeitschfrit für Physik und Mathematik (Johann-Gottlieb-Heubner (1778-1859) puis Carl Gerold (1783-1854)) – se contentent d’une insertion dir des planches [24] collées sans décalage avec la tranche du livre ce qui génère des difficultés de lecture puisque nous ne pouvons pas avoir simultanément le texte renvoyant à la figure et la figure elle-même. De plus, les rédacteurs Baumgartner et Ettingshausen cherchent à minimiser l’introduction de planches. Leur premier volume du Zeitschrift für Physik und Mathematik (1826) ne comporte qu’une seule planche comptant une trentaine de petites figures tassées les unes contre les autres.
L’examen des autres tomes confirme cette impression initiale. Ce choix semble également prévaloir dans le Journal de Crelle [25]. Cette politique d’insertion de planches (de quelques figures) en fin de cahier [26] ou de volume semble être le choix de toute la littérature mathématique allemande tout au long de la première moitié du XIXe siècle. En 1841, les Archiv der Mathematik und Physik procèdent comme dans le Journal de Crelle. La page de titre du volume relié de 1841 annonce en sous-titre que le texte est accompagné de « Mit vier lithographirten Tafeln und zwei Holzschnitten » [Avec quatre planches et deux gravures sur bois]. C’est exactement la même formulation pour le Zeitschrift für Mathematik und Physik en 1856. Il est simplement précisé que le volume est accompagné de neuf planches et gravures sur bois.
Discontinuités éditoriales au sein de la Correspondance mathématique
et physique de Quetelet
Pour la Correspondance de Quetelet, nous possédons plus d’informations sur la réalisation des planches. Au départ, en 1825, il y a manifestement une volonté d’insérer, dans le corps du texte, les figures élémentaires. Le premier théorème, un article de géométrie du co-fondateur Garnier, est illustré par une figure (fig. 3).
[16] J. Duchesne, Jean dit Duchesne ainé, Encyclopédie moderne : dictionnaire abrégé des sciences, des lettres, des arts, de l’industrie, de l’agriculture et du commerce, tome 16 (Fraude-Grégorien); sous la direction de M. Léon Renier, 1861-1865, Paris, Firmin Didot frères, pp. 654-662. Notons qu’il s’agit d’une nouvelle version d’éditions antérieures. En 1861-1865, Duchesne est déjà décédé depuis 1855.
[17] Pour avoir des informations sur Abraham Bosse, nous renvoyons à J. P. Le Goff, « Le cas Abraham Bosse », Cahiers de la perspective, Caen, IREM de Basse-Normandie, 2 (1982).
[18] Edité par Emery en 1701, ce Traité est considérablement augmenté en 1745, A. Bosse, De la Manière de graver à l’eau forte et au burin et de la gravure en manière noire, avec la façon de construire les presses modernes et d’imprimer en taille douce, Paris, Jombert, 1745. L’éditeur Charles-Antoine Jombert a conçu une nouvelle édition revue corrigée, augmentée du double et enrichie de dix-neuf planches en taille-douce. Bosse livre un manuel pratique sur l’art de la taille-douce à l’eau forte. Son ouvrage est une présentation technique et pragmatique constituée d’une succession de réponses techniques qu’il classe selon quatre parties : de la gravure au vernis dur, de la gravure au vernis mol, de la gravure au burin et de la manière d’imprimer en taille-douce, & de construire des presses. Bosse détaille tous les aspects techniques de la gravure (composition du vernis, choix du cuivre, du burin, etc.).
[19] Les numérisations publiées par google.books sont précieuses car il s’agit de numérisations brutes et exhaustives.
[20] A. Moatti, Le mystère Coriolis, Paris, CNRS Editions, 2014.
[21] Christian Gérini nous a indiqué que le fonds ancien de l’Université de Montpellier possède une planche originale de Gergonne, sous forme d’une plaque de cuivre gravée.
[22] C. von Wurzbach, Biographisches Lexikon des Kaiserthums Oesterreich, Band 2, Wien, 1857.
[23] F. von Burg, « Beweis für das Kräfteparallelogramm, auf blosses Raisonnement gegründet », Journal für diereine und angewandte Mathematik, 1 (1826), p. 369.
[24] Elles sont gravées par Michael Aigner (1805 - ?) jusqu’en 1829 puis de 1827 à 1832 par Mathias Bauer.
[25] Le premier tome (1826) ne compte qu’une seule planche de 12 figures sans mention de l’auteur. Cette direction éditoriale est ensuite poursuivie : nous comptons une planche de cinq figures dans le tome II, aucune planche dans le tome III, une planche de cinq figures dans le tome IV, aucune dans le suivant, etc.
[26] Nous rappelons ici que chaque tome annuel est divisé en quatre cahiers. Un cahier correspond à un découpage trimestriel. Notons que les tables récapitulatives de Crelle (A. L. Crelle, « Inhaltsverzeichnissen der Bände 1-50 dieses Journals, welche mit thätiger Beförderung hoher Königlich-Preufsischer Behörden in den Jahren 1826-1855 herausgegeben wurden, von Dr. August Leopold Crelle », Journal für die reine und angewandte Mathematik, 50 (1855), pp. 327-392) ne mentionnent pas les planches géométriques.


