
Formuler la vie – Entre écriture et image,
le dispositif des formules mathématiques
dans le récit de soi
- Odile Chatirichvili
_______________________________

Fig. 7. E. Frenkel, Love and Math..., 2013 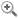
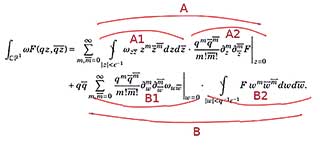
Fig. 8. E. Frenkel, Love and Math..., 2013 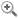

Fig. 9. E. Frenkel, Love and Math..., 2013 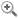

L’effet de suspens de la cataphore et des deux points se double d’un délai « matériel », puisqu’il faut tourner la page pour découvrir à quoi réfère le démonstratif, et que c’est alors seulement que la formule est révélée, en haut de la page suivante (fig. 7).
Cette formule a une signification mathématique, qui fait l’objet d’un développement dans le reste de la page : Frenkel y évoque son contexte éditorial et scientifique. Mais aucun lien n’est fait entre cette signification et la pertinence de choisir cet ensemble spécifique de notations mathématiques comme « formule de l’amour ». L’auteur n’explicite pas en quoi la formule choisie est « esthétiquement belle », ne thématisant même pas la subjectivité de son propre attrait esthétique pour la dimension graphique de ce qu’il produit.
En observant la formule, on peut noter la prépondérance de formes courbes, de symboles symétriques et de répétitions produites par le dédoublement de plusieurs lettres, créant un rythme visuel et une structure graphique harmonieuse. Ces effets de répétitions et de symétries se retrouvent dans la structure globale de la formule : après le signe « = », les deux lignes A et B constituent deux termes d’une somme (le signe « + » est en début de deuxième ligne). Chacun de ces deux termes est lui-même constitué de la multiplication de deux parties (séparées par un point de multiplication). La première partie et la deuxième partie de la ligne A ont respectivement la même forme que la deuxième partie et la première partie de la ligne B. Cette structure, correspondant à des conventions formelles en analyse, forme un chiasme syntaxique et visuel (fig. 8), une régularité symétrique perceptible par l’œil expert, et peut-être aussi, avec un peu d’attention, par l’œil inexpérimenté [49].
Outre la beauté esthétique de sa forme, cette formule présente, selon Frenkel, l’intérêt de l’hermétisme (« forbidding enough » / « l’effrayante formule » [50]) que le dispositif du tatouage est supposé contourner. L’usage du tatouage est justifié par Frenkel : certes, la formule est impénétrable, mais le scénario vise à susciter chez les spectateurs une réaction d’intérêt voire de passion que la même succession de signes inscrite sur un tableau noir n’aurait pas suscitée. La formule est choisie en dépit de (ou à cause de) son aspect illisible pour un public profane, clairement visé. Le procédé est celui de la recherche d’une réaction précise par l’articulation de l’incompréhension et de l’attraction.
Dans la suite du récit, Frenkel explique que, pour la réalisation du film, la notation devait se conformer aux exigences pratiques du tatouage afin de rester lisible sur l’espace limité de l’emplacement choisi. En résulte un processus de simplification de l’écriture formulaire, évoqué mais non expliqué. On n’en voit que le résultat final, selon le même procédé d’expérience spatiale de la page : un élément cataphorique (« here’s how it appears in our film: » / « voici comment elle apparaît dans le film » [51]) en bas de page délinéarise le processus de mise en scène du résultat final que l’on découvre en haut de page suivante (fig. 9).
La mise en page ainsi réalisée met en regard, dans l’espace de la double page, les deux formules (fig. 10).
Ainsi placées à la même hauteur, côte à côte, on peut aisément les percevoir d’un seul coup d’œil horizontal. A gauche, l’exactitude mathématique ; à droite, la forme adaptée nécessaire pour le film, informée par des exigences techniques et artistiques étrangères aux mathématiques. Or, le choix volontaire d’une formule complexe, l’absence d’explications (comme cela peut être le cas dans les chapitres précédents) et cet effet de miroir sur l’espace de la double-page font en sorte que la formule « fait image » : elle produit pour le lecteur un effet visuel (de surprise, d’incompréhension, de curiosité) fondé sur ses propriétés graphiques et le fait qu’elle allie calligraphie et changement d’alphabet. Il me semble que cette formule a, dans le livre, une fonction iconique au même titre que les photogrammes du film ; elle est en effet mise en valeur d’une manière très similaire à celle des images. Elle participe de la même élaboration esthétique qui met de côté sa signification mathématique au profit d’une dimension graphique fondée sur la mise en scène du couple, du double, de la symétrie en miroir des motifs et des dispositifs de mise en page.
L’imaginaire du matériau est également mis au travail ; d’un support immédiat (le papier du livre qu’on est en train de lire, sur lequel sont tracés les signes), on passe à un système de supports médiatisés : l’encre et le papier du livre servent à la reproduction de signes tracés par l’encre du tatouage sur la peau humaine, lesquels font écho aux motifs de la calligraphie, aux idéogrammes et aux variations d’alphabets (latin / cyrillique) qui traversent l’ensemble du court-métrage et le chapitre qui l’évoque. Ce dix-huitième chapitre a la fonction d’une clef de voûte narrative, dans et par laquelle le mathématicien-écrivain noue ses deux objectifs : raconter sa vie (du moins certains aspects et événements) et faire découvrir et aimer les mathématiques au plus grand nombre. Le texte, évoquant le film, fait jouer simultanément l’intention revendiquée d’expliquer, de faire comprendre, de rendre intelligible les mathématiques (champ de la raison) et une rhétorique récurrente, omniprésente de l’affectivité et de l’érotisme, de la beauté et de la splendeur des mathématiques présentées comme imposantes, au sens où elles ne peuvent que s’imposer. Double paradoxe : d’une part, le court-métrage met en scène non la figure potentiellement autobiographique du mathématicien contemporain professionnel, au travail, avec ses attributs habituels (craie et tableau noir [52] ou ordinateur ; solitude et incompétence sociale [53]), mais une figure fictionnelle, fictive, métaphorique voire allégorique, celle du personnage du « Mathématicien » passionné, amoureux, maudit, proche de l’imaginaire de l’artiste. D’autre part, l’approche des mathématiques se fait sous l’angle, non de la rigueur et de la scientificité, mais de l’affectivité dans son expression la plus charnelle. Le rapport d’autorité instauré par rapport au lecteur/spectateur profane en est radicalement modifié.
« Deuxième livre » et image de soi : reformulation
Dans les productions écrites d’un mathématicien, l’autobiographie joue un rôle proche de ce que Vincent Debaene appelle le « deuxième livre » [54] à propos de l’œuvre écrite des ethnologues : un livre « littéraire », ou tout du moins éloigné des règles formelles et méthodologiques en vigueur dans le champ scientifique, publié parallèlement à un ou des ouvrages techniques plus difficilement accessibles à la compréhension d’un lecteur profane. La présence de mathématiques dans le récit de vie des mathématiciens est paradoxale : les formules sont à la fois indispensables pour se dire (en tant que mathématicien) et incompréhensibles pour la plupart des lecteurs, au point qu’elles troublent la lecture en échappant aux mécanismes habituels de la lisibilité.
En comparant le recours aux formules chez Schwartz et chez Frenkel, il est possible d’esquisser une pensée des modes de perception et réception qui vont du lisible au visible : de la démonstration formulaire « sèche » ou glosée par l’écrit à diverses modalités de mise en valeur de la forme, signifiante ou non.
Pour le lecteur comme pour l’auteur, les formules sont doublement des images : représentations condensées d’une pensée mathématique qui définit en grande partie l’identité du mathématicien ; structures graphiques et symboliques nécessitant une compétence particulière pour être perçues comme signifiantes. Frenkel joue de cette dimension picturale et hermétique. La « formule de l’amour », telle qu’elle est incluse dans son autobiographie, est isolée spatialement et syntaxiquement. Le lecteur est invité à la voir, la regarder, l’admirer, plutôt qu’à la lire ou à la comprendre. Mais cet exemple est un cas particulier. Au sein même de Love and Math, le dispositif de la formule de l’amour est un hapax : elle est la seule à ne pas être présentée par l’auteur avec un appareil explicatif destiné à « équiper » le lecteur des connaissances promises – là où Schwartz, prenant acte d’une possible incompétence et faisant preuve d’un certain élitisme, ne semble pas s’embarrasser de ce genre d’effort mais présente un récit mathématique bien plus proche de son expérience de la recherche.
Ce rapport aux formules, cas particulier de l’inclusion des mathématiques dans ces textes, met en lumière des images de soi, recherchées ou non. Frenkel élabore, selon les moments, un ethos de pédagogue désireux de rendre accessible les mathématiques, et de créateur jouant de l’incompréhension pour élaborer une forme particulière de pouvoir : la formule mathématique devient formule magique. Schwartz, évoquant en Avant-propos son vœu de faire « entendre le timbre de sa voix » [55], propose des formes exigeantes hybridant le récit et la démonstration mathématique. Dans les deux cas, la dimension graphique est utilisée pour appuyer l’importance de l’oralité et de la relation de transmission au sein de la communauté mathématique et en dehors.
**
Bibliographie
- Abragam Anatole, De la physique avant toute chose ?, Paris, Odile Jacob, 1987.
- Barany Michael J., Mathematical Research in Context. (Dissertation submitted for the degree of MSc by research in Science & Technology Studies), University of Edinburgh, 2010.
- Barany Michael J. et MacKenzie Donald, « Chalk: Materials and Concepts in Mathematics Research », dans Catelijne Coopman, Janet Vertesi, Michaeland Lynch et Steve Woolgar (éd.), Representation in Scientific Practice Revisited, The MIT Press, 2014, p. 107-129.
- Chatirichvili Odile, « Désordres de la recherche dans les autobiographies de mathématiciens », dans B. Barbalato (dir.), Auto/biographie, désordre, entropie. Mnemosyne o la costruzione del senso, n°12, Presses universitaires de Louvain, 2019, p. 69-87.
- Debaene Vincent, L’adieu au voyage : l’ethnologie française entre science et littérature, Paris, Gallimard, 2010.
- Dotson Daniel, « Portrayal of Mathematicians in Fictional Works », CLCWeb: Comparative Literature and Culture, vol. 8, no 4, 2006 (consulté le 19 mars 2020).
- Eco Umberto, Lector in fabula, Paris, Grasset, 1985.
- Frenkel Edward, Love and Math: the Heart of Hidden Reality, New York, Basic Books, 2013.
- —, Amour et maths, Olivier Courcelle (trad.), Paris, Flammarion, 2015.
- Goldenstein Jean-Pierre, « Images de textes », dans Liliane Louvel et Henri Scepi (éd.), Texte / Image : nouveaux problèmes. Colloque de Cerisy, Rennes, Presses universitaires de Rennes, 2005, p. 378.
- Jeannelle Jean-Louis, Ecrire ses mémoires au XXe siècle : déclin et renouveau, Paris, Gallimard, 2008.
- Lafforgue Laurent, « Les mathématiques sont-elles une langue ? », colloque organisé à la BnF, Paris, 2005 (consulté le 19 mars 2020).
- Lejeune Philippe, Le Pacte autobiographique, Paris, Seuil, 1975.
- Rotman Brian, Mathematics as sign: writing, imaging, counting, Stanford Univ. Press, 2000.
- Schwartz Laurent, Un Mathématicien aux prises avec le siècle, Paris, Odile Jacob, 1997.
- Suchet Myriam, L’Imaginaire hétérolingue : ce que nous apprennent les textes à la croisée des langues, Paris, Classiques Garnier, 2014.
[50] E. Frenkel, Love and math, Op. cit., p. 238 ; E. Frenkel, Amour et maths, Op. cit., p. 298.
[51] E. Frenkel, Love and math, Op. cit., p. 238 ; E. Frenkel, Amour et maths, Op. cit., p. 299.
[52] Au sujet de l’influence des outils matériels sur le travail et les représentations des mathématiciens, voir M. J. Barany et D. MacKenzie, « Chalk: Materials and Concepts in Mathematics Research », dans C. Coopman et al. (éd.), Representation in Scientific Practice Revisited, s. l., The MIT Press, 2014, pp. 107-129.
[53] Au sujet de la représentation des mathématiciens dans l’imaginaire culturel, et notamment les œuvres de fiction mais aussi les œuvres biographiques, voir D. Dotson, « Portrayal of Mathematicians in Fictional Works », CLCWeb: Comparative Literature and Culture, vol. 8, n° 4, 1e décembre 2006.
[54] V. Debaene, L’Adieu au voyage : l’ethnologie française entre science et littérature, Paris, Gallimard, 2010.
[55] L. Schwartz, Un mathématicien aux prises avec le siècle, Op. cit., p. 10.