[7] Sur la cosmologie médiévale, voir toujours A. Koyré, Du monde clos à l'univers infini, Paris, Gallimard, « Tel », 1973, et plus récemment M.-P. Lerner, Le Monde des sphères, 2 vol., Paris, Belles Lettres, 2008.
[8] Victor Hugo, « La Caravane », dans Les Châtiments, VII, 8, Paris, Flammarion, 1998, p. 304. Voir aussi Pierre Reverdy : « Point de fuite jamais atteint, voilà le but — et, pousser l'horizon, jusqu'à ce qu'il nous engloutisse, notre implacable destinée » (Le Livre de mon bord, Paris, Mercure de France, 1970, p. 7, cité dans M. Collot, La poésie moderne et la structure d’horizon, Paris, PUF, 2005, p. 66).
[9] Sur cette question, parmi une vaste bibliographie, voir en particulier J. Wirth, L’Image à l'époque gothique (1140-1280), Paris, Editions du Cerf, 2008.
[10] Sur cet aspect voir déjà F. Botana, Learning through Images in the Italian Renaissance, Op. cit., pp. 200-201.
[11] L. Thorndike, The Sphere of Sacrobosco and its commentators, Chicago, The University of Chicago Press, 1949. Sur les figures, voir en particulier K. Müller, Visuelle Weltaneignung: astronomische und kosmologische Diagramme in Handschriften des Mittelalters, Göttingen, Vandenhoeck & Ruprecht, 2008.

L’image de l’horizon dans
la Sfera de Gregorio Dati
- Thomas Le Gouge
_______________________________

Fig. 1. G. Dati, La Sfera, XVe s. 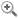

Fig. 2. G. Dati, La Sfera, 1470-1480 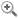

Fig. 3. G. Dati, La Sfera, fin du XVe s. 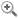

Fig. 4. J. de Sacrobosco, De sphaera, fin du XIIIe s. 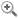

Fig. 5. Ioannis de Sacro Bosco Sphericum
opusculum, 1485 

L’expérience sensible que propose Dati semble certes accessible à tout un chacun, elle s’inscrit pourtant dans l’imaginaire scientifique de son temps. Pour s’imaginer percevoir l’horizon comme une ligne qui sépare le monde en deux hémisphères, il faut en effet concevoir l’univers comme une sphère occupée en son centre par le globe terrestre et non comme un espace infini dont l’horizon ne saurait être considéré que comme une limite relative à un certain point de vue [7]. L’idée selon laquelle l’horizon serait une limite inatteignable, une ligne vers laquelle, comme l’écrivait Hugo, « on avance toujours, on n’arrive jamais » [8], n’entre pas dans le contexte imaginaire de la fin du Moyen Age. Au contraire à cette époque l’horizon est une ligne située à un endroit bien précis.
L’illustration qui accompagne la description de Dati peut sembler à première vue paradoxale (fig. 1). Bien que le texte consiste en la mise en scène du regard d’un observateur, elle ne se présente pas sous la forme d’une représentation du ciel tel qu’on pourrait l’observer mais d’une figure géométrique qu’on pourrait presque trouver dans les Eléments d’Euclide. Le cercle périphérique représente le ciel, tandis que le plus petit cercle, au centre, représente la terre ; l’horizon enfin est figuré par le diamètre qui coupe le ciel et la terre en deux moitiés égales. Les segments qui partent de la surface de la terre indiquent le regard qu’un observateur situé sur la terre porte sur l’horizon.
Dans de nombreux manuscrits l’enlumineur a ajouté un soleil au zénith et a peint la partie inférieure en bleu, tandis que la terre, au centre, est peinte en noir et blanc. Les inscriptions « hémisphère éclairé », « hémisphère obscur » et « horizon » achèvent la figure. On retrouve le même chromatisme dans de nombreux manuscrits de la Sfera, bien que parfois la partie supérieure soit peinte en jaune ou en or (fig. 2), ou que l’ensemble de la sphère soit peint en bleu et blanc en imitant les couleurs du ciel (fig. 3). La manière dont les enlumineurs ont choisi d’orner la figure géométrique de l’horizon et de la colorer témoigne d’une volonté de l’associer à une réalité visible et sensible, comme si le diagramme astronomique sous-jacent, qui n’a à l’origine que pour fonction de montrer que la ligne d’horizon sépare le ciel et la terre en deux moitiés égales, servait désormais à représenter le ciel tel qu’on est supposé pouvoir le voir.
Par-là, Dati et les enlumineurs de la Sfera font un usage très particulier des diagrammes astronomiques qui s’inscrit dans une lente évolution qui remonte au début du XIIIe siècle, moment où les sciences basées sur l’observation des phénomènes comme l’optique (perspectiva) et l’astronomie connaissent des développements majeurs grâce aux traductions arabo-latines, et où l’image connaît en parallèle des changements qui l’orientent vers davantage de naturalisme [9]. Mais deux siècles plus tard, Dati mêle différentes sources, comme le montre d’une manière exemplaire l’illustration du passage sur l’horizon.
D’abord, la figure géométrique à la base de cette illustration est reprise littéralement du De sphaera de Sacrobosco [10]. Ecrit dans le deuxième quart du XIIIe siècle à Paris, ce manuel d’astronomie destiné aux étudiants fut diffusé jusqu’au XVIe siècle, copié dans des centaines de manuscrits, imprimé à de multiples reprises dès la fin du XVe siècle et très souvent accompagné de figures [11]. Dans le De sphaera, plusieurs passages évoquent l’horizon et Dati en a choisi un bien spécifique qui est loin d’être le plus courant.
La plupart du temps en effet, l’horizon désigne chez Sacrobosco la ligne de référence qui sert à déterminer la position des astres. Or cette ligne, explique-t-il, change en fonction de l’endroit où l’on se trouve sur la terre. Dans cette figure (fig. 4) en effet, Rome se trouve juste en-dessous du zénith et le diamètre du cercle désigne son « horizon », tandis que Paris se trouve sur la droite et son horizon est désigné par un diamètre oblique. Ceci permet de remarquer que lorsqu’il y a une éclipse de lune, elle apparaît d’abord aux Romains avant d’apparaître aux Parisiens. Dans cette autre figure (fig. 5), plus simple, nous voyons trois villes ayant chacune un horizon différent, qui marque chaque fois le début du jour et le début de la nuit. Ces observations visent à prouver, dans le De sphaera, que la terre est ronde et que le soleil tourne autour de la terre, car si la terre était plate, il ferait jour au même moment pour tous les habitants de la terre. Elles s’inscrivent plus généralement dans les définitions fondamentales déjà données par Ptolémée et reprises par Sacrobosco visant à distinguer ceux qui ont l’horizon « droit » et l’horizon « oblique » (fig. 6). Ceux qui ont l’horizon droit sont ceux qui habitent au niveau de l’équateur et dont l’horizon se confond avec la ligne qui passe par les pôles nord et sud ; cet horizon est dit « droit » car il est alors perpendiculaire à l’équateur. Ceux qui ont l’horizon oblique sont tous les autres, dont l’intersection de l’horizon et de l’équateur forme un angle non droit. Ces définitions et ces trois figures définissent ainsi l’horizon comme une ligne relative à la position qu’on occupe sur la terre.
Mais dans un autre passage du De sphaera, qui fut illustré dans des manuscrits datant, pour les plus anciens, du troisième quart du XIIIe siècle, Sacrobosco, à la suite de Ptolémée, veut prouver que la terre est au centre de l’univers à partir de l’évidence selon laquelle on voit toujours l’horizon couper l’univers en deux moitiés égales (fig. 7  ). Pour cela il mêle, là encore, figures géométriques et observations visuelles. Dans la première figure, tout en haut, Sacrobosco part d’une observation toute simple : lorsque le soleil est à son lever, au zénith ou à son coucher, il est toujours de la même taille. Or, dans un cercle, les segments qui partent du centre et vont vers la périphérie sont tous égaux. Donc, si le soleil, lors de son parcours, est toujours à la même distance de la terre, la terre est forcément au centre du ciel. Dans les deux figures suivantes, il poursuit sa démonstration en présentant deux situations impossibles. Dans la deuxième figure en effet, il montre que si la terre n’était pas au milieu du ciel, l’horizon ne couperait pas la terre et le ciel en deux moitiés égales ; or c’est contraire à l’observation et à ce que disent « tous les philosophes », écrit Sacrobosco : la nuit, on voit toujours six des douze signes du zodiaque. Dans la troisième figure, il soulève une objection : ceci ne prouve rien, car la terre n’est pas comme le point central d’un cercle, elle est un peu plus grande. Si bien que, comme le montre la figure, lorsqu’on dessine la terre comme un petit cercle, celui qui regardera vers le ciel la ligne d’horizon ne verra pas la moitié de l’univers, mais un peu moins, ce qui est impossible. La quatrième figure vient enfin résoudre le problème : comparée au ciel, la taille de la terre est incommensurable, elle est « comme un point » par rapport au ciel. Que l’on se trouve au centre géométrique de la figure ou à la surface du petit cercle, cela ne change rien, notre regard se porte toujours vers l’horizon qui sépare l’univers en deux moitiés égales. La terre est donc bien au centre de l’univers, comme le montre cette démonstration géométrique, qui s’appuie sur des observations visuelles.
). Pour cela il mêle, là encore, figures géométriques et observations visuelles. Dans la première figure, tout en haut, Sacrobosco part d’une observation toute simple : lorsque le soleil est à son lever, au zénith ou à son coucher, il est toujours de la même taille. Or, dans un cercle, les segments qui partent du centre et vont vers la périphérie sont tous égaux. Donc, si le soleil, lors de son parcours, est toujours à la même distance de la terre, la terre est forcément au centre du ciel. Dans les deux figures suivantes, il poursuit sa démonstration en présentant deux situations impossibles. Dans la deuxième figure en effet, il montre que si la terre n’était pas au milieu du ciel, l’horizon ne couperait pas la terre et le ciel en deux moitiés égales ; or c’est contraire à l’observation et à ce que disent « tous les philosophes », écrit Sacrobosco : la nuit, on voit toujours six des douze signes du zodiaque. Dans la troisième figure, il soulève une objection : ceci ne prouve rien, car la terre n’est pas comme le point central d’un cercle, elle est un peu plus grande. Si bien que, comme le montre la figure, lorsqu’on dessine la terre comme un petit cercle, celui qui regardera vers le ciel la ligne d’horizon ne verra pas la moitié de l’univers, mais un peu moins, ce qui est impossible. La quatrième figure vient enfin résoudre le problème : comparée au ciel, la taille de la terre est incommensurable, elle est « comme un point » par rapport au ciel. Que l’on se trouve au centre géométrique de la figure ou à la surface du petit cercle, cela ne change rien, notre regard se porte toujours vers l’horizon qui sépare l’univers en deux moitiés égales. La terre est donc bien au centre de l’univers, comme le montre cette démonstration géométrique, qui s’appuie sur des observations visuelles.